그래프란?
그래프는 정점과 간선으로 이루어진 자료구조이다. 정확히는 정점(Vertex)간의 관계를 표현하는 조직도라고 볼 수도 있다. 그런 면에서 트리는 그래프의 일종인 셈이다. 다만 트리와는 달리 그래프는 정점마다 간선이 없을 수도 있고 있을 수도 있으며 루트 노드, 부모와 자식이라는 개념이 존재하지 않는다. 또한 그래프는 네트워크 모델 즉, 객체와 이에 대한 관계를 나타내는 유연한 방식으로 이해할 수 있다. 실생활에서 다양한 예를 그래프로 표현할 수 있다. 대표적으로 지하철 노선도, 도심의 도로 등이 있다. 이런 식으로 활용할 수 있는 방법이 많기에 문제도 다양하게 출제를 할 수 있다. 그래프는 알고리즘에서 굉장히 많이 사용된다. 특히 그래프를 순회하는 방식인 DFS와 BFS를 잘 알아두어야 한다.
그래프에서 사용하는 용어

정점(vertice) : 노드(node)라고도 하며 정점에는 데이터가 저장된다. (0, 1, 2, 3)
간선(edge): 링크(arcs)라고도 하며 노드간의 관계를 나타낸다.
인접 정점(adjacent vertex) : 간선에 의해 연결된 정점으로 위에서 (정점 0과 정점 1은 인접 정점)
단순 경로(simple-path): 경로 중 반복되는 정점이 없는것, 같은 간선을 자나 가지 않는 경로.
차수(degree): 무방향 그래프에서 하나의 정점에 인접한 정점의 수. (정점 0의 차수는 3)
진출 차수(out-degree) : 방향그래프에서 사용되는 용어로 한 노드에서 외부로 향하는 간선의 수를 뜻한다.
진입 차수(in-degree) : 방향그래프에서 사용되는 용어로 외부 노드에서 들어오는 간선의 수를 뜻한다.
그래프 구현 방법
그래프를 구현하는 방법에는 인접 행렬(Adjacency Materix)와 인접 리스트(Adjacency List) 방식이 있다. 두 개의 구현 방식은 각각의 상반된 장단점을 가지고 있는데 대부분 인접 리스트 형식을 많이들 사용한다.
인접행렬(Adjacency Materix)
- 두 정점을 바로 이어 주는 간선이 있다면 "두 정점은 인접하다"라고 표현한다.
- 인접 행렬은 서로 다른 정점들이 인접한 상태인지를 표시한 행렬로, 2차원 배열의 형태로 나타낸다.
- 만약 1이라는 정점과 2라는 정점이 이어져 있다면 1(true), 이어져 있지 않다면 0(false)으로 표시한 일종의 표이다.
- 만약 가중치 그래프라면, 1 대신 관계에서 의미 있는 값을 저장한다.

인접행렬 장점
1. 2차원 배열 안에 모든 정점들의 간선 정보를 담기 때문에 배열의 위치를 확인하면 두 점에 대한 연결 정보를 조회할 때 O(1) 의 시간 복잡도면 가능하다.
2. 구현이 비교적 간편하다.
인접행렬 단점
1. 모든 정점에 대해 간선 정보를 대입해야 하므로 O(n²) 의 시간 복잡도가 소요된다.
2. 무조건 2차원 배열이 필요하기에 필요 이상의 공간이 낭비된다.
인접행렬은 언제 사용할까?
- 인접 행렬은 한 개의 큰 표와 같은 모습을 하고 있다. 이러한 표는 두 정점 사이에 관계가 있는지, 없는지 확인하기에 용이하다.
예를 들어, 1에서 2로 진출하는 간선이 있는지 파악하기 위해선 0번째 줄의 1번째 열에 어떤 값이 저장되어 있는지 바로 확인할 수 있다. - 가장 빠른 경로(shortest path)를 찾고자 할 때 주로 사용된다.
인접리스트(Adjacency List)
- 인접 리스트는 각 정점이 어떤 정점과 인접한지를 리스트의 형태로 표현한 것이다.
- 각 정점마다 하나의 리스트를 가지고 있다.
- 이러한 하나의 리스트는 자신과 인접한 다른 정점을 담고 있다.

인접리스트 장점
1. 정점들의 연결 정보를 탐색할 때 O(n) 의 시간이면 가능하다. (n: 간선의 갯수)
2. 필요한 만큼의 공간만 사용하기 때문에 공간의 낭비가 적다.
인접리스트 단점
1. 특정 두 점이 연결되었는지 확인하려면 인접 행렬에 비해 시간이 오래 걸린다. (배열보다 search 속도 느림)
2. 구현이 비교적 어렵다.
인접리스트는 언제 사용할까?
- 메모리를 효율적으로 사용하고 싶을 때, 인접 리스트를 사용
(인접 행렬은 연결 가능한 모든 경우의 수를 저장하기 때문에 상대적으로 메모리를 많이 차지한다.)
다양한 그래프의 종류
1) 무방향 그래프(Undirected Graph)
두 정점 사이에 존재하는 간선을 나타낼 때 간선의 방향이 없는 그래프.

2) 방향 그래프(Directed Graph)
두 정점 사이에 존재하는 간선을 나타낼 때 간선의 방향이 존재하는 그래프.

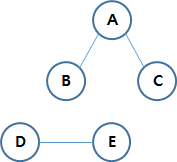
3) 연결 그래프(Connected Graph)
그래프에서 어떤 정점에서 다른 정점까지 갈 수 있는 경로가 존재하면 두 정점은 연결되었다고 한다.
모든 정점들에 대해서 어느 두 정점을 잡아도 갈 수 있는 경로가 존재하는 그래프가 연결 그래프(Connected Graph)이다. 그 반대는 단절 그래프(비 연결 그래프, Disconnected Graph)이다.
방향 그래프에서 임의의 두 정점 x, y에 대하여 x에서 y로 갈 수 있는 경로가 존재하고 아울러 y에서 x로 갈 수 있는 경로가 존재하면 이것을 강력 연결 그래프(Strongly Connected Graph)라 한다.
4) 다중 그래프(Multi Graph)
보통 그래프라고 하면 두 정점 사이의 간선은 무방향 그래프일 때는 한 개가
존재하고, 방향 그래프일 때는 두 개까지 존재할 수 있다.
그러나 두 정점 사이에 두 개 이상의 간선이 존재하는 그래프를 다중 그래프(multigraph)라고 한다.
일반적으로 그래프라고 하면 다중 그래프는 포함하지 않는다.
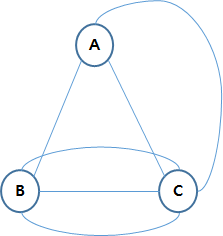
정점 A와 C 사이에 간선 2개
정점 B와 C 사이에 간선 3개
5) 완전 그래프(Completed Graph)
n개의 정점을 갖는 무방향 그래프에서 간선의 최대 수는 n(n-1)/2이다.
n개의 정점을 갖는 방향 그래프에서 간선의 최대 수는 n(n-1)이다.
어떤 그래프의 간선수가 최대 간선수를 가졌다면 이를 완전 그래프(completed graph)
라고 한다.
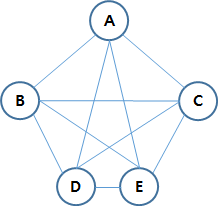
정점이 5인 무방향 그래프의
최대 간선수는 5(5-1)/2 =10개이다.
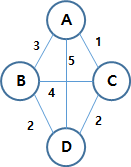
6) 가중 그래프(Weighted Graph)
정점을 연결하는 간선에 가중치를 부여한 그래프로, 네트워크(Network)라고도 한다.
예를 들어 정점을 도시, 간선을 도로라고 하면, 간선에 부여된 가중치는 통행료, 이동 시간 등이 될 수 있다.
// 가중 그래프에서 최단 거리(가중치의 최소)를 구하기 위한 다익스트라(Dijkstra) 알고리즘이 있다.
**다익스트라는 추후 업로드 예정이다.
그래프의 탐색
첫 정점에서부터 그래프에 존재하는 모든 정점들을 모두 한 번씩 방문하는 것을 그래프 탐색이라고 한다. 그래프 탐색의 방법은 깊이 우성 탐색(DFS) 방식과 너비 우선 탐색(BFS) 방식이 있다.
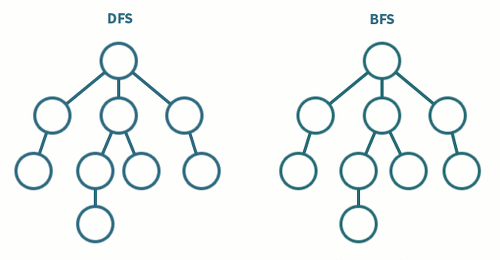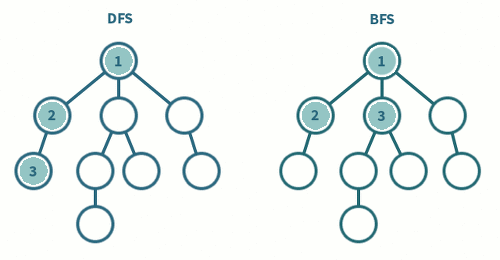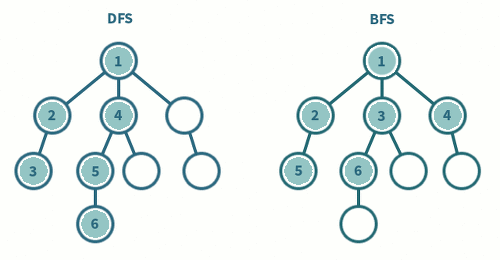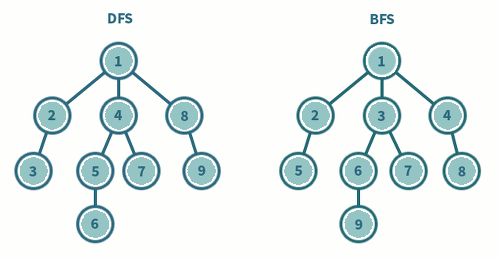
깊이 우선 탐색(DFS)
깊이 우선 탐색 DFS는 갈 수 있는 만큼 최대한 깊이 가고, 더 이상 갈 곳이 없다면 이전 정점으로 돌아가는 방식으로 그래프를 순회하는 방식이다. 간단히 재귀 호출을 사용하여 구현하거나 스택을 사용하여 구현한다.
넓이 우선 탐색(BFS)
넓이 우선 탐색 BFS는 시작 정점을 방문한 후 시작 정점에 인접한 모든 정점을 방문한 후 시작 정점에 인접한 모든 정점들을 우선 방문하는 방법이다. 일반적으로 QUEUE를 사용해서 지금 위치에서 갈 수 있는 것들을 모두 큐에 넣는 방식으로 구현한다.
Reference
'Algorithm & Data Structure > study' 카테고리의 다른 글
| [Algorithm / Java] ✒️ Insertion Sort(삽입 정렬) (0) | 2022.08.16 |
|---|---|
| [Algorithm / Java] ✒️ Selection Sort(선택 정렬) (0) | 2022.08.16 |
| [Algorithm / Java] ✒️ Bubble Sort (거품 정렬) (0) | 2022.08.15 |
| [Data Structure / Java] ✒️ Vector (0) | 2022.08.15 |
| [Data Structure / Java] ✒️ Stack, Queue (0) | 2022.08.15 |