[Data Structure / Java] ✒️ Tree(트리)

Tree란?

비선형(Non-Linear)자료 구조이다. 이러한 구조는 단일 방향으로 각각의 데이터들이 연결되거나 나열된 것이 아니라 복수의 데이터들이 복수의 데이터들과 연결될 수 있는 구조로 설계될 수 있다.

 

선형 구조와 비-선형 구조의 차이

Point	선형 구조	비-선형 구조
데이터 저장	순차적으로 각 데이터를 순회할 수 있도록 저장	데이터들이 계층적으로 연결되어 저장
수준(Level)	단일 수준(Level)에서 모든 데이터를 저장	복수 수준(Level)에서 데이터를 저장
구현 복잡도	구현이 쉬움	구현이 어렵고 이해도 난해
순회	단일 동작으로 모든 데이터 순차적 순회 가능	데이터 순회에 복수의 동작 필요
메모리 활용	메모리 공간 활용 효율성 낮음	메모리 공간을 매우 효율적으로 활용
시간 복잡도	저장 공간이 늘어나면 비례하여 증가	저장 공간이 늘어나면 비례하는 수준보다 적게 증가

 

아래처럼 가족 관계도를 그릴 때 트리 형식으로 나타내는 경우도 많이 봤을 것이다. 자료구조의 트리도 이 방식을 그대로 구현한 것이다.

 

Tree를 이해하기 가장 쉬운 구조는 집안의 계보이다. 조상님부터 대대로 내려오는 계보를 보면 어떠한 구조로 집안 내력이 형성되어 있는지를 명료하게 알 수 있을 것이다. 누가 어느 집안 사람인지, 몇 번째 자식인지 등등..

혹은 회사의 조직 구조도를 보면 된다. 누가 어디 조직에 소속되어 있는지, 조직 간 연결 구조는 어떠한지 매우 명료하게 확인할 수 있다.

 

https://hongjw1938.tistory.com/18

위 그림은 대표적인 Tree 형태의 구조를 의미한다. 각각이 의 노드가 있고 이 노드들이 각각 2개의 노드와 연결되어 있다. 이러한 구조를 이진 트리(Binary Tree) 라고 한다. 

 

이름	설명	위 그림 기반 예시
Root	Tree 구조의 최상단 Node	Node1
Edge	Node와 Node의 연결	화살표
Parent	Leaf Node 제외한 모든 Node Edge로 연결된 Node를 하위에 보유한 모든 Node	Node1 ~ 3
Child	Root Node를 제외한 모든 Node 즉, Parent를 갖는 Node	Node2 ~ 7
Leaf	Tree의 구조에서 Child를 갖지 않는 모든 최하단 Node	Node4 ~ 7
Height	전체 Tree 구조에서 가장 긴 경로	Root - Leaf 모든 경로가 2의 거리(경로)
Depth	특정 Node에서 Root Node 까지의 경로(깊이)	Node3은 Root 까지 1의 Depth
Sub Tree	Tree 구조 내에 있는 모든 부분적인 Tree들	Node2와 그 아래는 전체 Tree의 Sub Tree
Sibling	동일한 Parent / Level 갖는 관계인 Node	Node2, Node3은 Sibling

트리의 Depth(깊이)는 루트를 0으로 두거나 1로 두는 경우가 있다. 반드시 정해진 것은 아님 

추가로, 조상(Ancestor), 자손(Descendent)도 있는데 이는 정점 A에서 정점 B사이를 루트를 경유하지 않고 위 혹은 아래 방향으로 한 방향으로만 이동이 가능할 때, A가 루트에 더 가깝다면 A를 조상, B를 자손이라고 부른다.

조상은 자기 자신을 포함하여 간주하기 때문에 자기 자신도 스스로의 조상이 된다고 본다.

 

참고로 Tree는 그래프의 일종.

그래프와 Tree의 차이

구분	그래프(Graph)	트리(Tree)
정의	객체 혹은 노드(Node)와 그것을 연결하는 간선(Edge)으로 모인 구조	그래프의 한 종류 방향성이 없으며 순환하지 않음
방향성	무방향 혹은 유방향으로 가능	무방향 그래프
순환성	순환 가능 자기 자신을 연결하는 간선(Self-Loop) 가능 순환(Cyclic), 비순환(Acyclic) 그래프 모두 가능	순환 불가능 자기 자신 연결 간선(Self-Loop) 불가능 비순환 그래프(Acyclic Graph)
루트	루트의 개념이 있거나 없을 수 있음	하나의 루트 노드 존재
모델	네트워크 모델	계층 모델
순회	넓이 우선 탐색(BFS) 깊이 우선 탐색(DFS)	전위(Pre) / 중위(In) / 후위(Post) 순회 방식
간선 수	그래프에 따라 다르며 없을 수도 있음	N개의 노드(Node)라면 N-1개

순회의 경우, 전위 / 중위 / 후위 순회방식은 기본적으로 DFS를 사용한 방식이라고 볼 수 있다. 트리는 그래프의 일종이므로 BFS / DFS로도 탐색은 가능하다.

 

Tree의 특징

• 트리에는 사이클이 존재할 수 없다. (만약 사이클이 만들어진다면, 그것은 트리가 아니고 그래프다)
• 모든 노드는 자료형으로 표현이 가능하다.
• 루트에서 한 노드로 가는 경로는 유일한 경로 뿐이다.
• 노드의 개수가 N개면, 간선은 N-1개를 가진다.

가장 중요한 것은, 그래프와 트리의 차이가 무엇인가인데, 이는 사이클의 유무로 설명할 수 있다.

 

Tree 순회 방식

트리를 순회하는 방식은 총 4가지가 있다.

https://github.com/gyoogle/tech-interview-for-developer/blob/master/Computer%20Science/Data%20Structure/Tree.md

 

1. 전위 순회(pre-order)

각 루트(Root)를 순차적으로 먼저 방문하는 방식이다.

(Root → 왼쪽 자식 → 오른쪽 자식)

1 → 2 → 4 → 8 → 9 → 5 → 10 → 11 → 3 → 6 → 13 → 7 → 14

 

2. 중위 순회(in-order)

왼쪽 하위 트리를 방문 후 루트(Root)를 방문하는 방식이다.

(왼쪽 자식 → Root → 오른쪽 자식)

8 → 4 → 9 → 2 → 10 → 5 → 11 → 1 → 6 → 13 → 3 →14 → 7

 

3. 후위 순회(post-order)

왼쪽 하위 트리부터 하위를 모두 방문 후 루트(Root)를 방문하는 방식이다.

(왼쪽 자식 → 오른쪽 자식 → Root)

8 → 9 → 4 → 10 → 11 → 5 → 2 → 13 → 6 → 14 → 7 → 3 → 1

 

4. 레벨 순회(level-order)

루트(Root)부터 계층 별로 방문하는 방식이다.

1 → 2 → 3 → 4 → 5 → 6 → 7 → 8 → 9 → 10 → 11 → 13 → 14

 

---

Binary Tree(이진 트리)

 이진트리는 각 노드가 Child 노드를 최대 2개씩 보유한 형태를 의미.

각 노드는 Left / Right Child 노드라고 명명해서 부른다. 위 그림에서 예시로 든 트리 형태 또한 이진 트리이다.

 

완전 이진 트리 / 포화 이진 트리

 이진 트리는 위의 그림과 같은데 그 중에서도 완전 이진 트리(Complete Binary Tree)와 포화 이진 트리(Perfect Binary Tree)가 있다.

 

완전 이진 트리는 위 층위부터 시작하여 왼쪽에서 오른쪽 방향으로 모든 노드가 차 있는 경우를 의미한다.
포화 이진 트리는 Leaf 노드가 있는 층위까지 모든 노드가 다 꽉 차 있는 상태를 의미한다.

 

https://hongjw1938.tistory.com/18

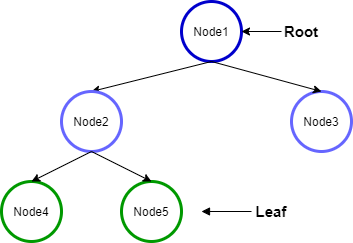
위 그림은 완전 이진 트리이다.

위 층위부터 아래 층위로 가면서 왼쪽부터 차곡차곡 쌓여 있기 때문이다.

https://hongjw1938.tistory.com/18

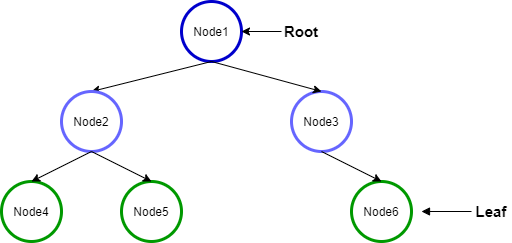
위 그림은 그냥 이진 트리일 뿐, 완전 이진 트리가 아니다.

왜냐하면 Node3의 자식이 좌측부터 채워지지 않았기 때문이다.

https://hongjw1938.tistory.com/18

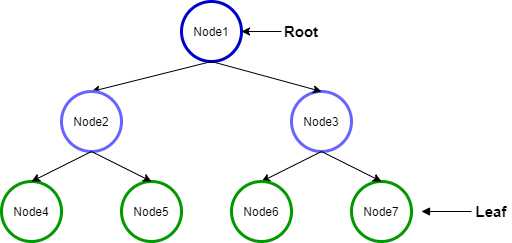
위 그림은 포화 이진 트리의 그림이다. 모든 층위에 노드가 꽉 차있기 때문이다.

이는 완전 이진 트리이기도 하다. 포화 이진 트리는 반드시 완전 이진 트리이지만 완전 이진 트리가 반드시 포화 이진 트리는 아니다.

 

Reference

• 겐지충 프로그래머 - 자료구조 - 트리(Tree), 이진트리(Binary Tree)
• Gyoogle / tech-interview-for-developer / Computer Science / Data Structure / Tree.md