Dijkstra 알고리즘
다익스트라(Dijkstra) 알고리즘은 방향성을 가지는 그래프에서 최단거리를 구할 때 자주 쓰인다.
방향성을 가지는 그래프란 A에서 B노드로 이동은 가능하지만, B노드에서 A노드로는 이동할 수 없는 경우가 있는 그래프를 말한다.
즉, 노드 간의 연결된 간선이 방향과 거리 비용을 가지고 있고, 시작 노드에서 다른 노드들까지의 최단거리 비용을 구할 때 사용할 수 있다.
Process
1. 거쳐 갈 혹은 시작할 노드를 방문 후 방문 처리한다.
2. 방문한 노드에서 이동할 수 있는 노드들을 탐색한다.
3. 탐색된 노드들의 계산된 거리 비용이 현재까지 저장된 최단거리보다 적을 경우 최단거리를 갱신한다.
4. 최단거리가 갱신된 노드들 중 가장 적은 거리를 가지는 노드로 이동 후 방문 처리한다.
5. 1~4번을 계속 반복 후 더 이상 방문할 노드가 없을 때 종료된다.
그림으로 알아보기
Ex)

위의 그래프를 보면 노드 간에 연결된 간선들이 방향성을 가지고 있고 각 간선들마다 거리 값이 있는 것을 알 수 있다.
출발 노드는 1번이고, 1번 노드에서 다른 노드들까지 이동할 때의 최단거리를 구한다고 가정하고 다익스트라(Dijkstra) 알고리즘을 진행해보겠다.

최초에 최단거리 테이블을 작성할 때 시작 노드를 제외한 모든 노드들의 최단거리 값은 INF이고 시작 노드의 값은 0으로 초기화된다. (INF값은 간선이 가질 수 있는 거리 비용의 최댓값보다 항상 크다고 가정합니다.)
2번과 3번 노드는 그래프에서 보시는 것처럼 각 간선의 거리 값으로 최단거리 테이블을 갱신해주었다.
4번과 5번 노드는 현재 1번 노드에서 방문할 수 없으므로 INF값으로 불가능을 나타내 주었다.
방문처리가 된 노드는 노란색으로 표시해줬다.
갱신 여부는 FALSE, TRUE로 표시해줬다.
이제 최단거리가 갱신된 노드들 중에서 가장 적은 최단거리를 가지는 노드로 이동한다.
위의 예시에서는 2번 노드가 3번 노드보다 값이 더 적으므로 2번 노드로 이동 후 방문 처리한다.

2번 노드를 방문한 후에는 이동 가능한 노드들을 탐색 후 최단거리 테이블을 갱신해줘야 한다.
현재 2번 노드에서 방문 가능한 노드는 3번과 4번 노드가 있다.
그러나 3번 노드는 1번->3번으로 갈 때의 거리 비용이 1번->2번->3번으로 이동할 때의 거리 비용 값보다 적으므로 갱신되지 않았다.
이를 최단거리 테이블 관점에서 살펴보면 다음과 같이 표현할 수 있다.
최단거리 테이블 3번 노드 값 < 최단거리 테이블 2번 노드 값 + 2번 노드에서 3번 노드로 이동할 때의 간선의 거리
결국 좌측의 값이 우측보다 클 때만 최단거리가 경신된다고 할 수 있다.
이어서 살펴보겠다.
4번 노드는 1번 노드에서 이동이 불가능했지만 2번 노드를 거쳐갈 때는 이동이 가능하므로 1번->2번->4번 노드로 연결되는 간선의 거리 비용 값을 모두 더한 값으로 갱신해준다.
이를 최단거리 테이블 관점에서 살펴보겠다.
최단거리 테이블 4번 노드 값 > 최단거리 테이블 2번 노드 값 + 2번 노드에서 4번 노드로 이동할 때의 간선의 거리
이번에는 좌측의 값이 우측의 값보다 크기 때문에 최단거리 테이블이 갱신되었다. (INF는 간선이 가질 수 있는 거리의 최댓값보다 큰 값이다.)
이제 최단거리가 갱신된 노드 중 가장 적은 거리를 가지는 노드로 이동 한다.
위의 그림에서는 1번 노드를 방문했을 때 갱신되었던 3번 노드가 4번 노드보다 거리 값이 적으므로 3번 노드로 이동 한다.

3번 노드를 방문 처리 후에 이동 가능한 노드를 탐색하면 현재 4번 노드로만 이동이 가능하다.
최단거리 테이블 갱신을 위해 최단거리 값을 계산해보겠다.
최단거리 테이블 4번 노드 값 < 최단거리 테이블 3번 노드 값 + 3번에서 4번 노드로 이동할 때의 거리
좌측의 값보다 우측의 값이 크기 때문에 4번 노드의 최단거리는 갱신되지 않는다.
이제 현재까지 최단거리가 갱신된 노드 중에서 거리가 가장 적은 노드로 이동을 진행한다.
현재 갱신된 노드 목록에서 남아있는 노드는 4번 노드 1개뿐이므로 4번으로 이동 한다.
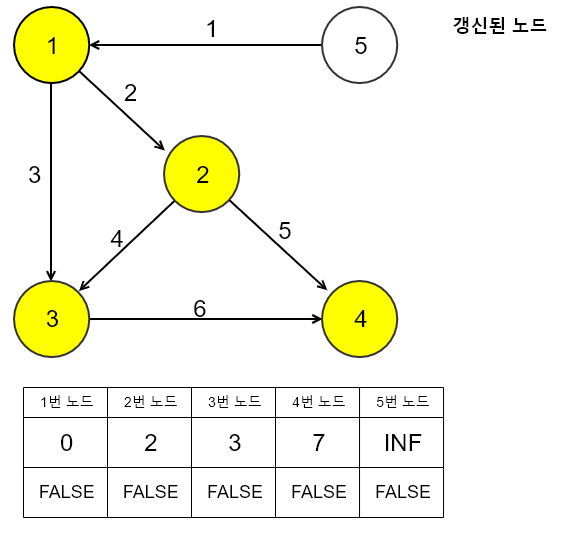
4번 노드를 방문 처리한 후에 이동 가능한 노드를 탐색한다.
현재 4번 노드에서 다른 노드들로 이동 가능한 간선이 존재하지 않기 때문에 최단거리 테이블을 갱신하는 작업은 진행되지 않는다.
다음으로 현재까지 갱신된 노드들 중에서 가장 적은 거리 값을 가지는 노드를 찾는다.
그러나 갱신된 노드 목록이 비어있으므로 더 이상 방문할 노드가 존재하지 않다는 걸 알 수 있다.
방문할 노드가 존재하지 않으면 알고리즘을 종료한다.
알고리즘이 종료된 시점에서 최단거리 테이블의 값은 시작 노드에서 다른 모든 노드들을 방문할 때의 최단거리를 의미한다.
위의 예시에서 5번 노드를 제외하고는 모두 방문이 가능했고, 5번 노드는 1번 노드에서 이동할 수 있는 방법이 없으므로 불가능을 의미하는 INF값을 가진다.
Code
1753번: 최단경로
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1 ≤ V ≤ 20,000, 1 ≤ E ≤ 300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1 ≤ K ≤ V)가
www.acmicpc.net
그래프를 표현하는 List와 우선순위 Queue에 모두 사용할 Node클래스
// 우선순위 큐에서 정렬기준을 잡기위해 Comparable를 구현합니다.
static class Node implements Comparable<Node>{
int index; // 노드 번호
int distacne; // 이동 할 노드까지의 거리
Node(int index, int distacne) {
this.index = index;
this.distacne = distacne;
}
// 최단거리를 기준으로 오름차순 정렬합니다.
@Override
public int compareTo(Node o) {
return Integer.compare(this.distacne, o.distacne);
}
}
main메서드와 함께 전체적인 소스
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.PriorityQueue;
public class BOJ_1753 {
// INF 값 초기화
static final int INF = 9999999;
// 그래프를 표현 할 2차원 List
static List<List<Node>> graph = new ArrayList<>();
// 최단거리테이블을 표현 할 배열
static int[] result;
// 방문처리를 위한 배열이지만 저는 다른 방법으로 방문처리를 진행하겠습니다.
// static boolean[] vistied;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
String[] info = br.readLine().split(" ");
int startIndex = Integer.parseInt(br.readLine());
// 그래프 생성
for (int i = 0; i < Integer.parseInt(info[0])+1; i++) {
graph.add(new ArrayList<>());
}
// 최단거리테이블 생성
result = new int[Integer.parseInt(info[0])+1];
// 최단거리테이블 INF로 초기화
Arrays.fill(result, INF);
// 방문처리를 위한 배열 생성 (저는 사용하지 않습니다)
// vistied = new boolean[Integer.parseInt(info[0])+1];
// 문제에서 주어진 입력 값에 따라 그래프 초기화
for (int i = 0; i < Integer.parseInt(info[1]); i++) {
String[] temp = br.readLine().split(" ");
graph.get(Integer.parseInt(temp[0])).add(new Node(Integer.parseInt(temp[1]), Integer.parseInt(temp[2])));
}
// 문제에서 주어진 입력값을 바탕으로 다익스트라 알고리즘 수행
dijkstra(startIndex);
// 문제에서 제시한 조건에 맞게 출력
for (int i = 1; i < result.length; i++) {
if(result[i] == INF) {
bw.write("INF");
bw.newLine();
}else {
bw.write(String.valueOf(result[i]));
bw.newLine();
}
}
bw.flush();
}
// 다익스트라 알고리즘
static void dijkstra(int index) {
// 최단거리가 갱신 된 노드들을 담을 우선순위 큐 생성
PriorityQueue<Node> pq = new PriorityQueue<>();
// 최단거리테이블의 시작지점노드 값 0으로 갱신
result[index] = 0;
// 우선순위 큐에 시작노드 넣기
pq.offer(new Node(index, 0));
// 우선순위 큐에 노드가 존재하면 계속 반복
while(!pq.isEmpty()) {
// 큐에서 노드 꺼내기
Node node = pq.poll();
// 꺼낸 노드의 인덱스 및 최단거리 비용 확인
int nodeIndex = node.index;
int distance = node.distacne;
// 앞에서 주석처리했던 방문처리 배열을 사용해서 아래와 같이 방문처리하셔도 됩니다.
// if(vistied[nodeIndex]) {
// continue;
// }else{
// vistied[nodeIndex] = true;
// }
// 큐에서 꺼낸 거리와 최단거리테이블의 값을 비교해서 방문처리를 합니다.
// 큐는 최단거리를 기준으로 오름차순 정렬되고 있습니다.
// 만약 현재 꺼낸 노드의 거리가 최단거리테이블의 값보다 크다면 해당 노드는 이전에 방문된 노드입니다.
// 그러므로 해당노드와 연결 된 노드를 탐색하지 않고 큐에서 다음 노드를 꺼냅니다.
if(distance > result[nodeIndex]) {
continue;
}
// 큐에서 꺼낸 노드에서 이동 가능 한 노드들을 탐색합니다.
for (Node linkedNode : graph.get(nodeIndex)) {
// 해당노드를 거쳐서 다음 노드로 이동 할 떄의 값이 다음 이동노드의 최단거리테이블 값보다 작을 때
if(distance + linkedNode.distacne < result[linkedNode.index]) {
// if문의 조건을 만족했다면 최단거리테이블의 값을 갱신합니다.
result[linkedNode.index] = distance + linkedNode.distacne;
// 갱신 된 노드를 우선순위 큐에 넣어줍니다.
pq.offer(new Node(linkedNode.index, result[linkedNode.index]));
}
}
}
}
// 우선순위 큐에서 정렬기준을 잡기위해 Comparable를 구현합니다.
static class Node implements Comparable<Node>{
int index; // 노드 번호
int distacne; // 이동 할 노드까지의 거리
Node(int index, int distacne) {
this.index = index;
this.distacne = distacne;
}
// 최단거리를 기준으로 오름차순 정렬합니다.
@Override
public int compareTo(Node o) {
return Integer.compare(this.distacne, o.distacne);
}
}
}
Reference
'Algorithm & Data Structure > study' 카테고리의 다른 글
| [Data Structure / Java] ✒️ HashMap (1) | 2022.08.18 |
|---|---|
| [Data Structure / Java] ✒️ Tree(트리) (0) | 2022.08.16 |
| [Algorithm / Java] ✒️ Quick Sort (퀵 정렬) (0) | 2022.08.16 |
| [Algorithm / Java] ✒️ Insertion Sort(삽입 정렬) (0) | 2022.08.16 |
| [Algorithm / Java] ✒️ Selection Sort(선택 정렬) (0) | 2022.08.16 |